Normalized Transformer

arXiv

We have been using transformers daily for a couple of years now, but the advancements on the architectural side have remained minimal. This paper from Nvidia proposes a normalized Transformer (nGPT), which performs representation learning on a hypersphere. Here is a summary for the same:

Token embeddings and output logits

1. Both input and output embedding matrices are normalized after each training step.
2. The logits are bounded in the range [-1, 1] because of the normalization, which limits the confidence of the probability distribution generated by the softmax.
3. To adjust this during training, the authors introduce a trainable scaling parameter sz that scales the logits element-wise.

Layers and Blocks

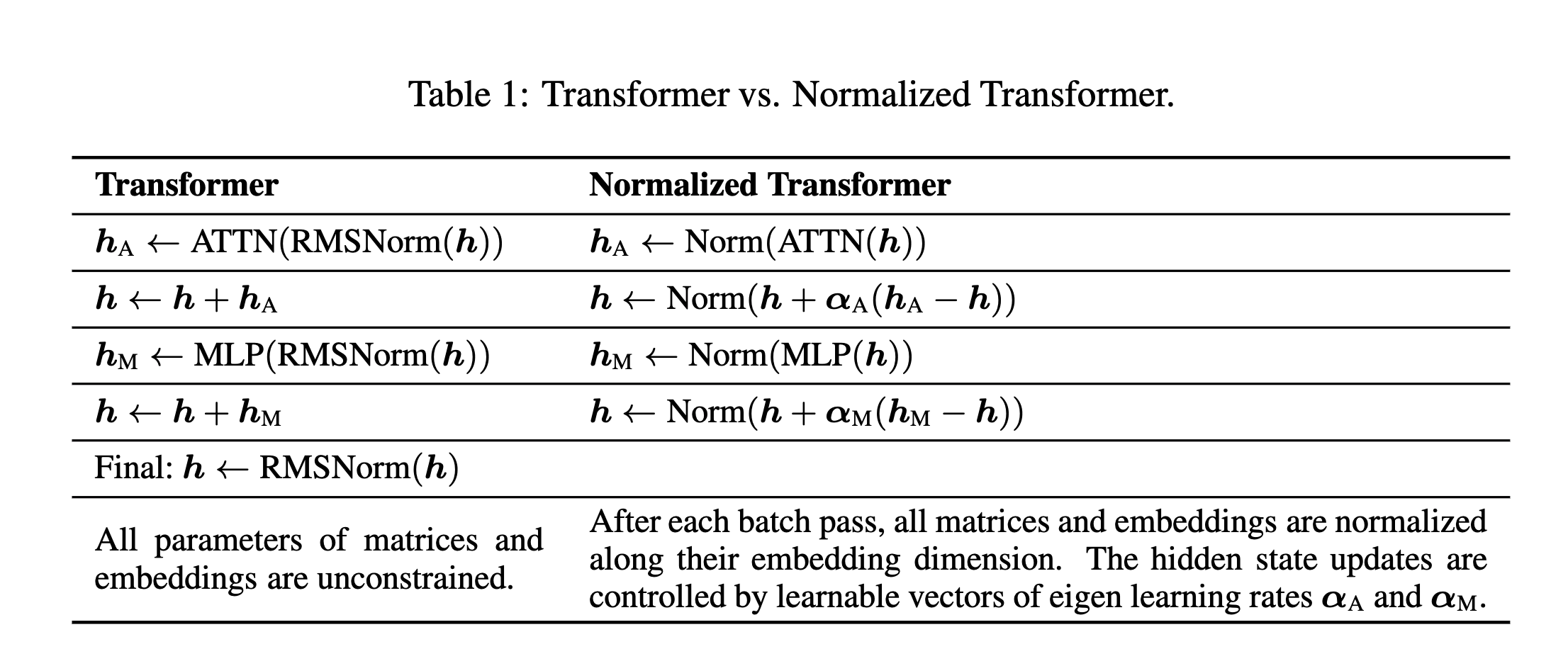
1. A typical transformer block looks like this where L layers of transformations are applied to the hidden state h, consisting of alternating the self-attention and MLP blocks:
   
   
   
   

2. If we are on a hypersphere, we can use spherical linear interpolation to compute the geodesic distance between two points a and b on the hypersphere. We can approximate SLERP with approximate linear interpolation (LERP) as shown below:
   
   
   
   

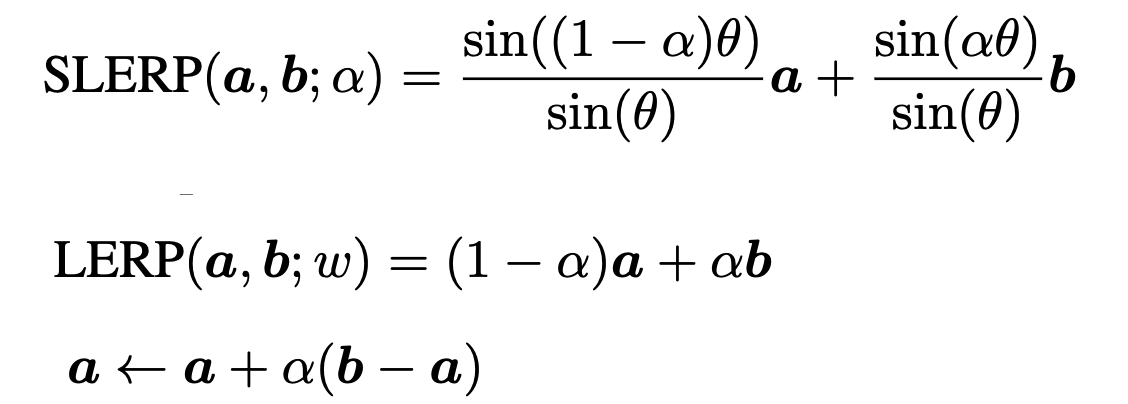
3. If point a is our hidden state h, and point b represents the point suggested by the attention or MLP block, we can represent our equations for the transformer blocks like this:
   
   
   
   

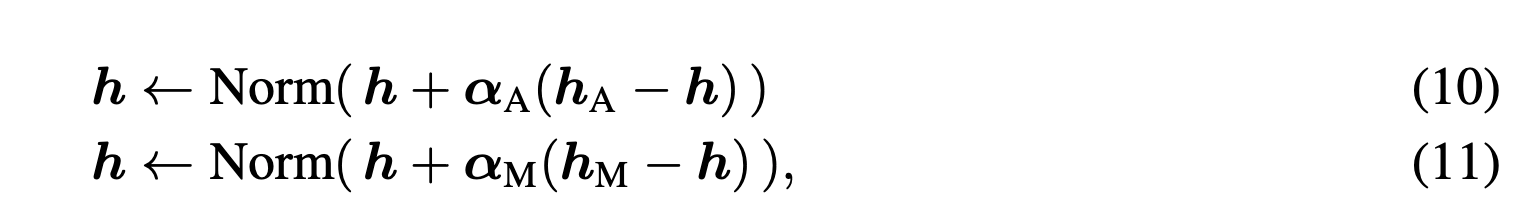
4. Here α_A ≥0 and α_M ≥0, with dimensionality d_model, are learnable parameters applied to the normalized outputs of the attention and MLP blocks, respectively. The norm function normalizes any vector x to have a unit norm and, unlike RMSNorm or LayerNorm, does not introduce any element-wise scaling factors. This normalization can be viewed as the retraction step in Riemannian optimization, mapping the updated solution back to the manifold.

Self-Attention Blocks

1. The qkv values produced by the weight matrics W_q, W_k, and W_v in the original transformer are unconstrained, leading to unbounded values in q.

2. In nGPT the authors normalize W_q, W_k, W_v and W_o along their embedding dimension so that the computed dot products with h can be interpreted as cosine similarity between unit norm vectors bounded in [−1, 1]. Thus, all attention matrices can be viewed as collections of normalized embedding vectors to be compared.

3. Though each element of q and k is now bounded, the norms of these two vectors can still vary. Also, the addition of positional embeddings can further distort q and k. To this end, the authors additionally normalize q and k by introducing a scaling factor s_qk for each head, ensuring that the dot product of every query and key is under control.

4. In the original Transformer, the query-key dot product is scaled by 1/√d_k before applying softmax to account for the expected variance of d_k in the dot product of non-normalized query and key vectors. In the normalized Transformer, the expected variance of the dot product between the normalized query and key vectors is 1/dk. The softmax scaling factor should instead be √d_k to restore a variance of 1

MLP

1. The input hidden state h of the MLP block of a classical transformer is first normalized using RMSNorm(or LayerNorm) and then passed through two separate linear projections, producing two intermediate vectors u and v, which are then combined using SwiGLU.

2. The weight matrices W_u and W_v in nGPT are normalized. The authors introduce scaling factors s_u and s_ν to control their impact. They also rescale ν by √d_model to optimize SiLU performance.

Summary of all modifications

1. Remove all normalization layers like RMSNorm or LayerNorm.

2. After each training step, normalize all matrices (E_input, E_output, W_q, W_k, W_v, W_o, W_u, W_ν, and W_o) along their embedding dimension.

3. Replace the updates as follows where α_A (and also α_M) is treated with α_A,init = 0.05 (in order of 1/n_layers) and α_A,scale = 1/√d_model.

4. Change the softmax scaling factor in attention from 1/√d_k to √d_k.

5. Implement the rescaling and normalization of q and k where s_qk is treated with s_qk,init = 1 and s_qk,scale = 1/√d_model.

6. Implement the rescaling of the intermediate state of the MLP block where s_u (and also s_ν) is treated with s_u,init = 1 and s_u,scale = 1

7. Implement the rescaling of logits using equation 3, where sz is treated with s_z,init = 1, s_z,scale = 1/√d_model.

8. Remove weight decay and learning rate warmup.

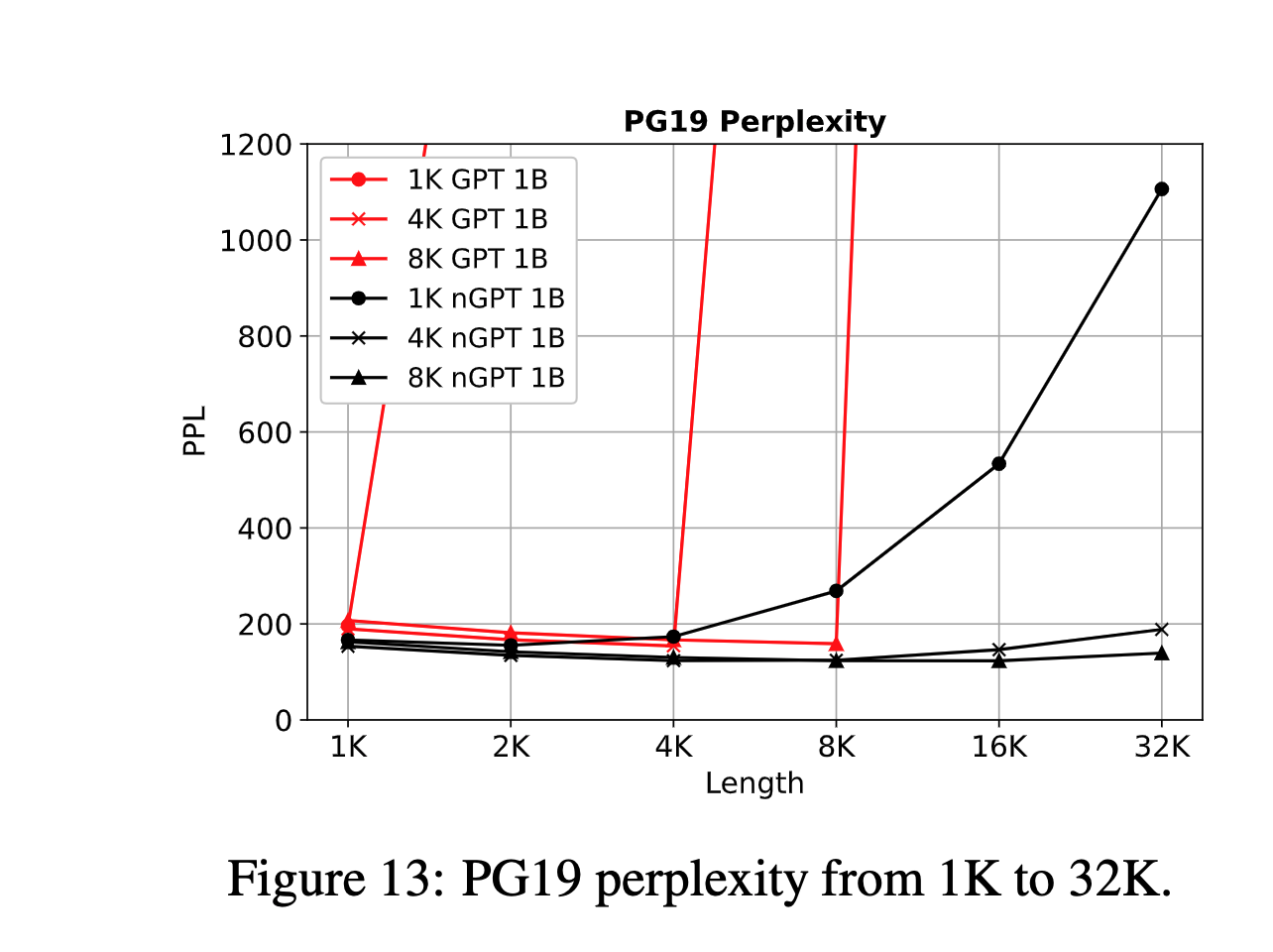
How fast is nGPT compared to GPT?

A lot! Training the 0.5B and 1B nGPT models is approximately 4x, 10x, and 20x faster at context lengths of 1k, 4k, and 8k tokens, respectively.

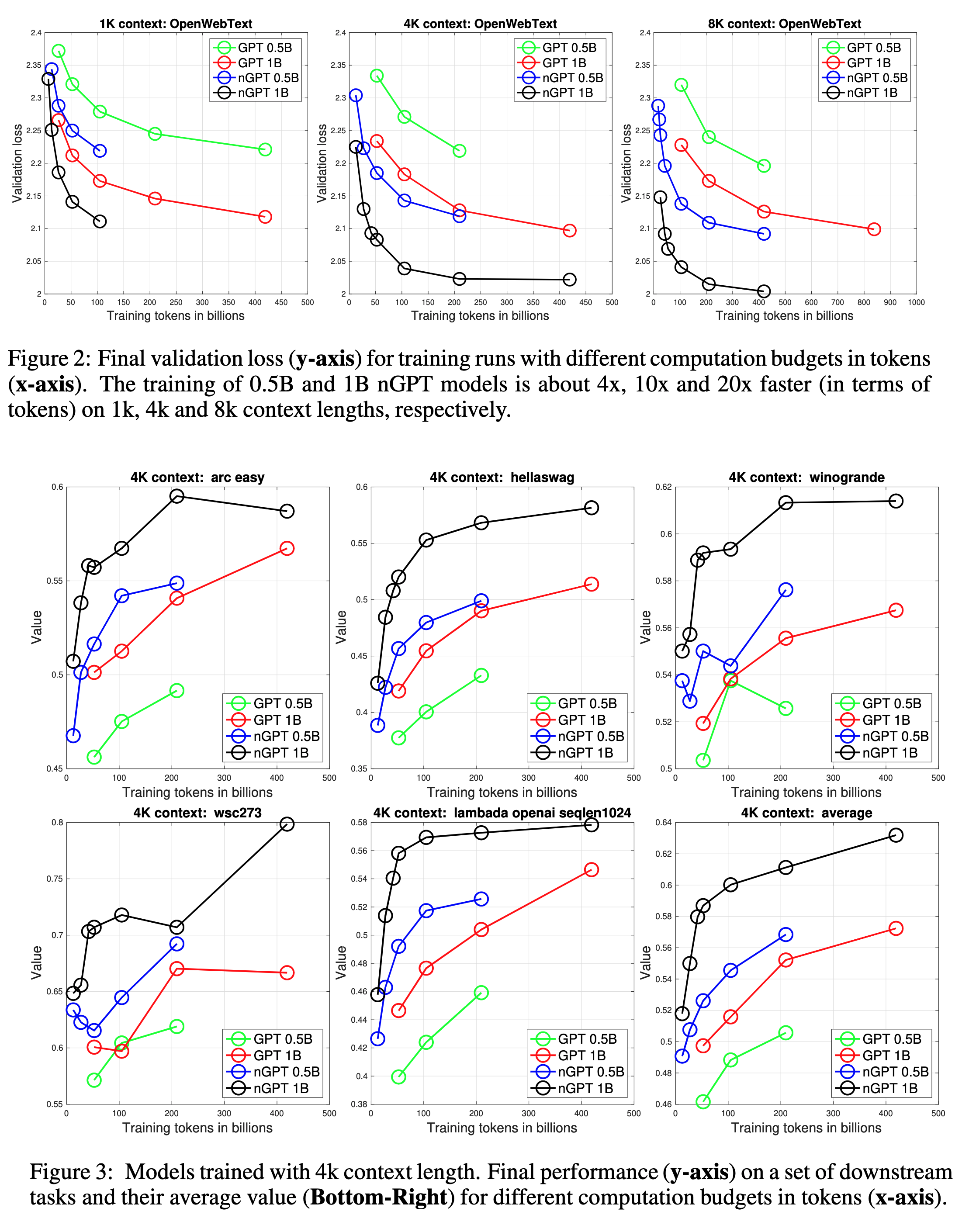
What about the params and hparams?

There should be a catch somewhere, right?

Of course, there is always a catch! Quoting directly from the paper: The time cost per step for nGPT is approximately 80% higher with a 4k context length, and 60% higher with an 8k context length. This overhead is not only due to nGPT having 6 normalization steps (2 of them are applied for q and k) per layer instead of 2 but also because nGPT’s normalizations are not yet fully optimized, unlike GPT, where normalization layers are fused with other operations.

Best thing about nGPT?

In standard GPTs, perplexity tends to increase dramatically when tested on sequences longer than pre-training length. In contrast, nGPT maintains a stable perplexity range even at extrapolated lengths.